[最も選択された] x y=6 x-y=2 graph 133711-Solve graphically x+y=6 x-y=2

Graph x^2=y^2z^2 Natural Language;

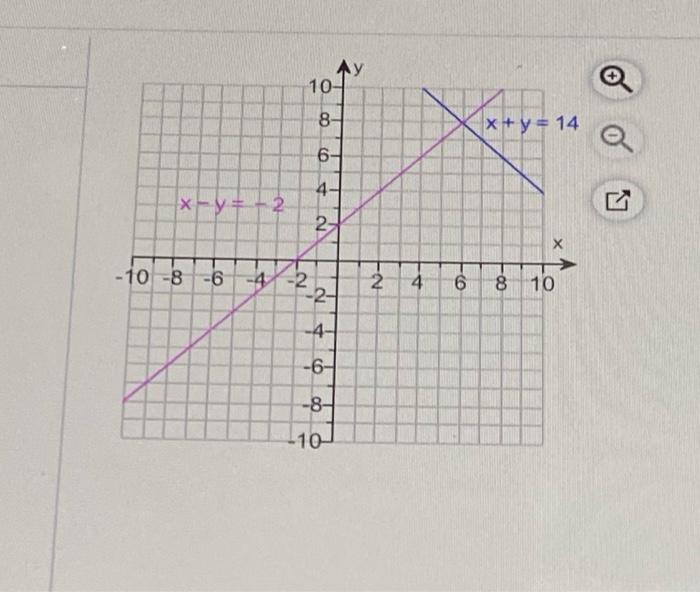
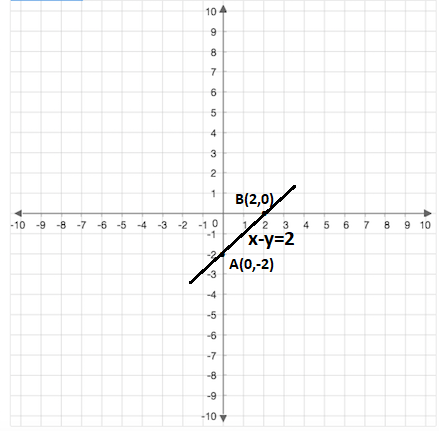
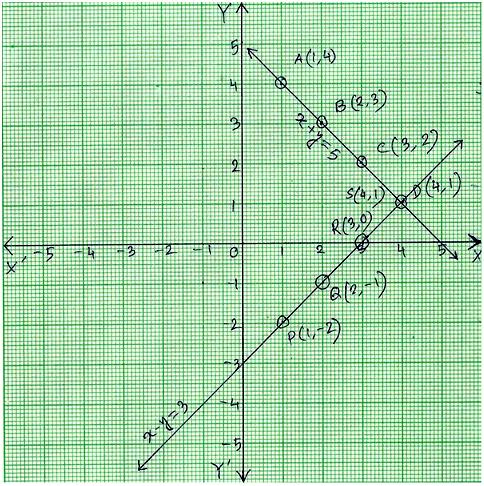
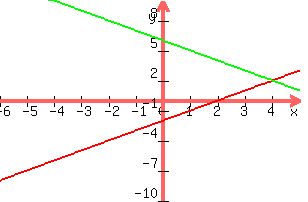
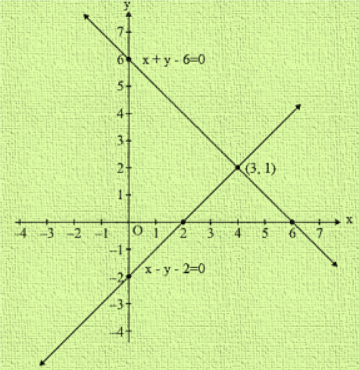
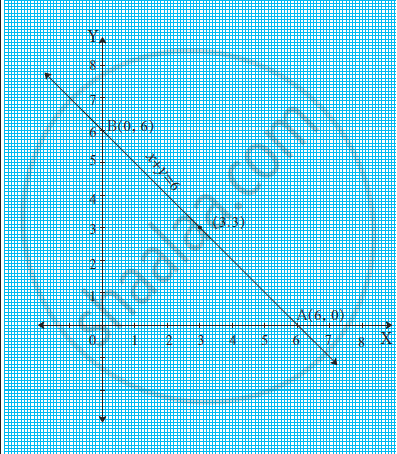
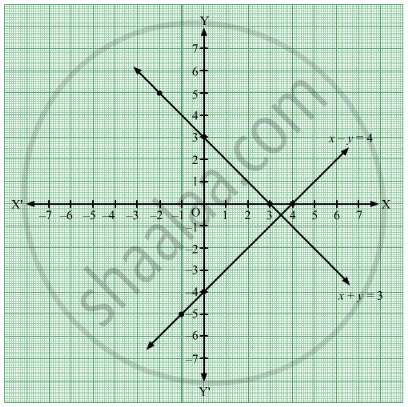
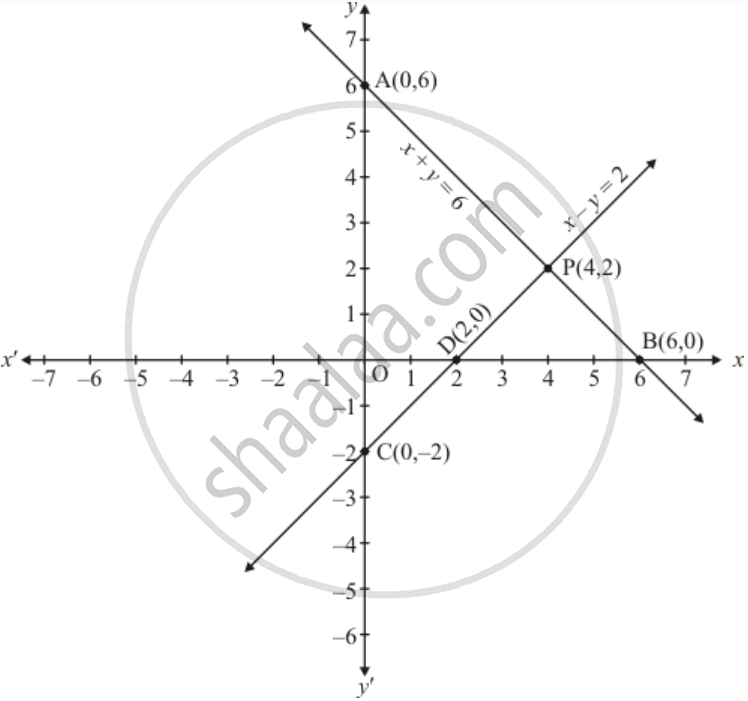
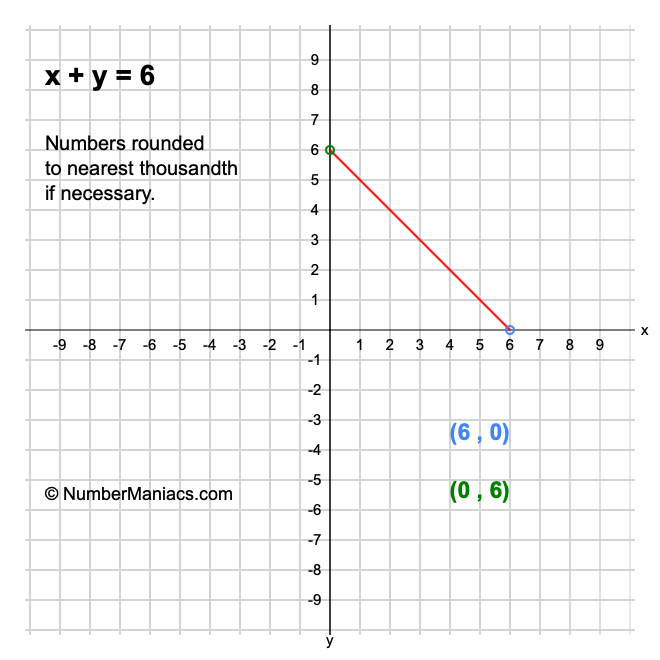
Solve graphically x+y=6 x-y=2-Put x 2y = 6 in slope intercept form 2y = x 6 y = 1/2 x 3 The equation tells me that the slope is shallow anf runs from quadrant II down through quadrant I, intersecting the y axis at 3 ForPlotting the points, the graph is obtained as follows We find that the line cuts the xaxis at a point P which ia at a distance of 3 units to the right of yaxis Therefore, the coordinates of P are (3, 0)

Solve graphically x+y=6 x-y=2のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Solve graphically x+y=6 x-y=2」の画像ギャラリー、詳細は各画像をクリックしてください。

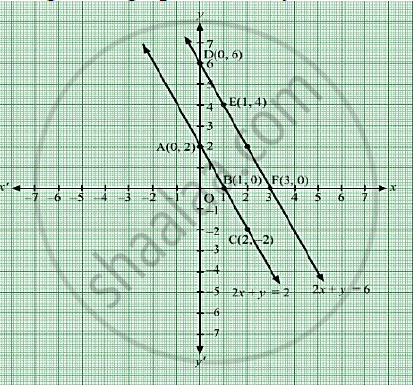
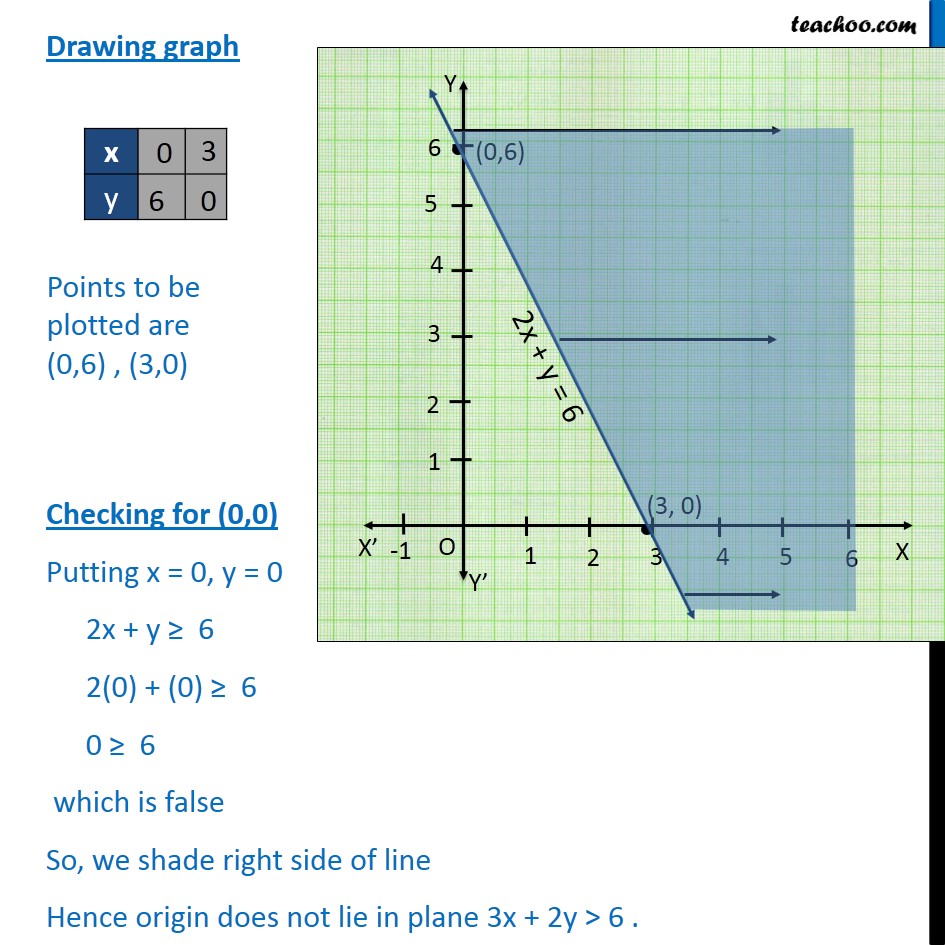
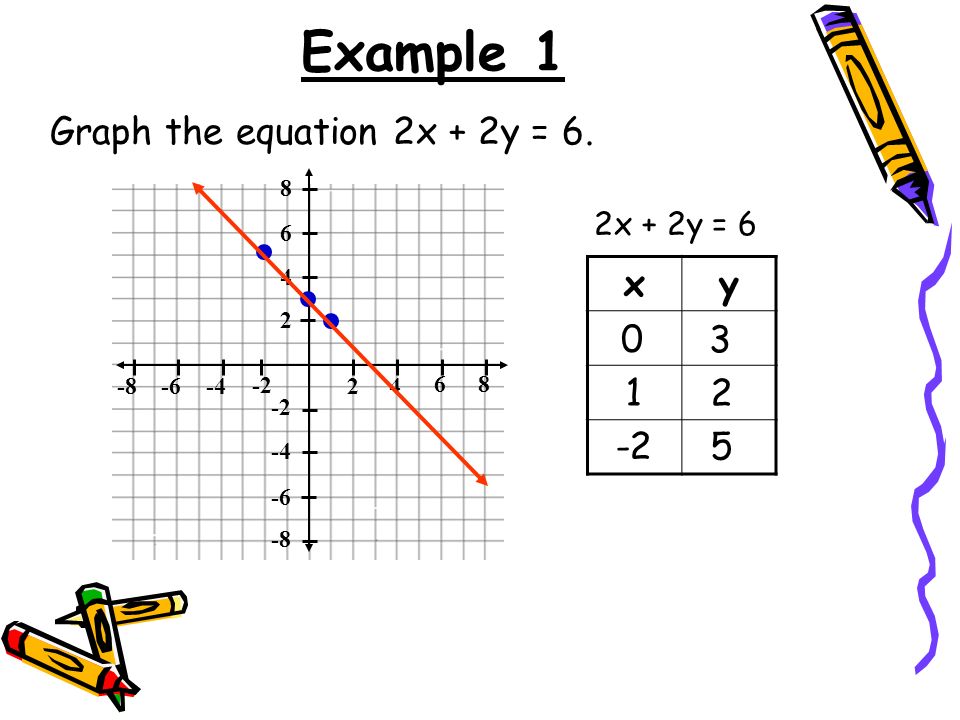
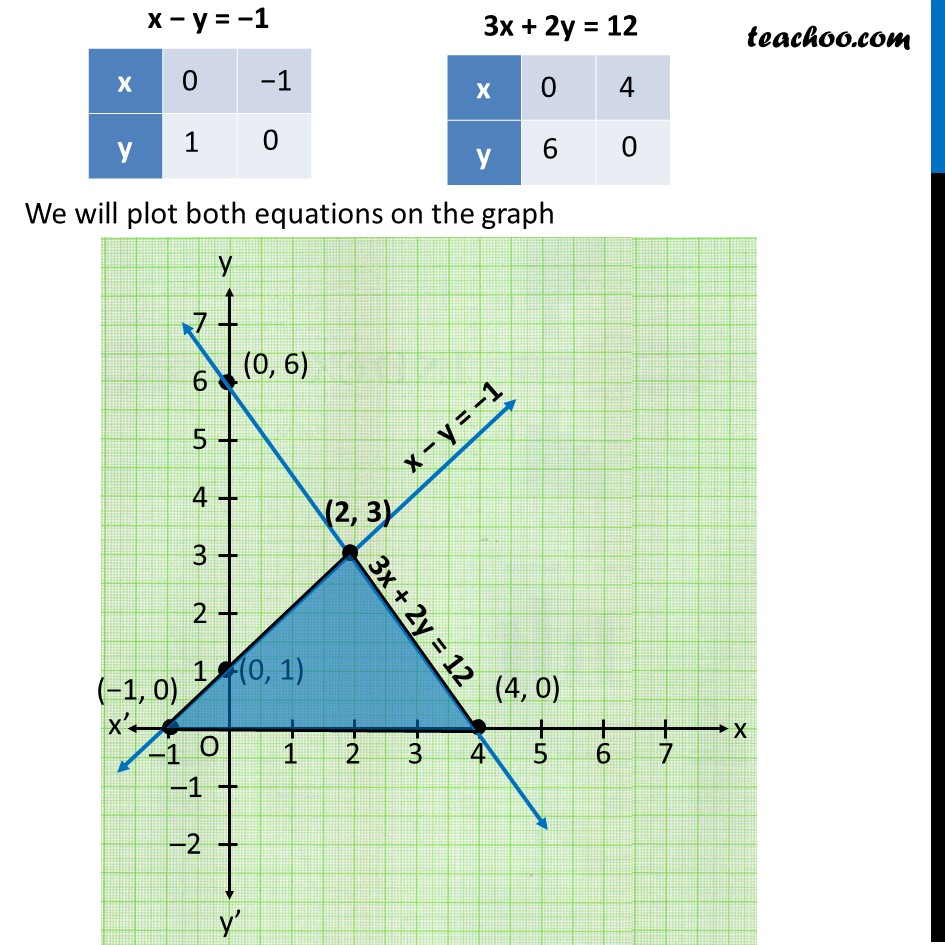
Question Draw the graph of 2xy=6 and 2x−y2=0 Shade the region bounded by these lines and x−y Find the area of the shaded region Hard Solution Verified by Toppr Sketching the Graph of an Equation by Point Plotting 1 If possible, rewrite the equation so that one of the variables is isolated on one side of the equation The equation is x y

Incoming Term: x+y=6 x-y=2 graph, solve graphically x+y=6 x-y=2,